INTRODUCTION

La scoliose est une déformation rachidienne caractérisée par une courbure dans le plan frontal, une déviation antéropostérieure surtout lordotique dans le plan sagittal et une rotation vertébrale dans le plan horizontal. La déformation du rachis dans l’un des plans spatiaux entraîne automatiquement une déformation dans les deux autres plans. Cette interaction dans le développement et la progression de la déformation est causée par l’effet de « coupling » qui s’explique par les liens musculaires et conjonctivaux des vertèbres [1]. Bien que les techniques chirurgicales employées actuellement ne soient pas basées sur la mesure et l’appréciation précises de la rotation, la quantification des éléments de la courbure et de la rotation vertébrale est importante dans la planification de l’intervention chirurgicale et l’appréciation des résultats [2].

Il est prouvé que la scoliose est une déformation 3D mais l’analyse des courbures de la colonne se réduit à la mesure des courbures frontales et sagittales. De nombreuses méthodes de mesure de la courbure frontale comme l’index Greespan [3], la méthode Diab [4] ou la méthode Centroid se sont développées [5]. Sur la proposition de Ferguson, la pratique la plus ancienne mesure l’angle formé par les droites reliant les points centraux des vertèbres-limites supérieure et inférieure et de la vertèbre apicale [6]. Pour l’analyse quantitative de la scoliose Cobb [7] propose la valeur de l’angle complémentaire déterminé par les perpendiculaires aux plateaux supérieurs et inférieurs des vertèbres-limites supérieure et inférieure. L’angle de Cobb mesure plutôt l’inclinaison des vertèbres et non la courbure de la colonne, il néglige la dérivation de la vertèbre apicale, pourtant courante dans les déformations rachidiennes. Bien que la méthode de Ferguson tienne compte de la dérivation, la méthode de Cobb est la plus utilisée pour sa facilité d’application, sa meilleure reproductivité et sa valeur angulaire fidèle à l’importance de la courbure.

Depuis la reconnaissance en 1966 par la Scoliosis Research Society (SRS) de la méthode de Cobb comme méthode standard, elle est devenue la méthode unique d’analyse quantitative de la déformation rachidienne.

Compte tenu des variations physiologiques relativement larges des courbures sagittales, l’analyse quantitative des courbures physiologiques accompagnant les scolioses reste difficile. Bien que Cobb élabore sa méthode dans le but d’analyser les courbures frontales, celle-ci devint très vite la méthode adaptée à l’analyse des courbures sagittales [8]. La méthode de Cobb, dans le plan sagittal également, analyse surtout l’inclinaison des plateaux supérieurs et inférieurs des vertèbreslimites et ne donne pas d’information concordante sur les déformations de la courbure [9]. Pourtant, dans les clichés du plan sagittal elle s’avère précieuse dans l’analyse de la cyphose dorsale [10] et la lordose lombaire [11], si l’on utilise des mesures uniformes.

Les variations de l’angle de Cobb dans la cyphose dorsale et la lordose lombaire accompagnant la scoliose structurale sont plutôt influencées par l’importance de la courbure dans le plan frontal et l’inclinaison du bassin dans le plan sagittal [12].

La recherche d’une analyse précise de la rotation vertébrale accompagnant la scoliose n’est pas nouvelle : de nombreuses méthodes ont été décrites par Cobb [7], Nash et Moe [13], Perdriolle [14] ou Mehta [15], elles se basent sur l’analyse de la position relative des différents éléments postérieurs de la vertèbre. Bien que dans la pratique clinique le torsiomètre de Perdriolle soit le plus utilisé, la reproduction de cette mesure de rotation est très limitée et ne peut être précisé- ment chiffrée [16].

L’utilisation du tomodensitomètre (TDM) et sa charge de rayon importante ne permet l’analyse de la rotation vertébrale au plan horizontal que sur un segment court de la colonne [17] et les professionnels mettent en doute la valeur de ces examens [18, 19].

Malgré l’affirmation en 1994 par le groupe de travail « 3D Terminology of Spinal Deformity » de la Scoliosis Research Society (SRS) selon laquelle il était souhaitable d’élaborer une nouvelle méthode dans le diagnostic et l’analyse des trois plans dans les déformations scoliotiques, cette aspiration resta théorique puisque l’on ne disposait pas de possibilité de mesure simultanée de la rotation vertébrale dans le plan horizontal et des courbures sagittale et frontale.

En 1992 Georges Charpak obtint le prix Nobel de Physique pour ses recherches dans le domaine de la détection des particules et la découverte des détecteurs gazeux [21, 22]. Un appareil basé sur cette nouvelle méthode de détection permet d’obtenir des radiographies de bonne qualité en économisant considérablement les doses des radiations [23].

De cette technologie est né un nouvel appareil d’imagerie médicale appelé EOS.

Cet appareil comporte une double innovation : il permet d’obtenir des images de très bonne qualité en 2D [24, 25] et également en 3D en position debout de l’ensemble du squelette de la tête aux pieds grâce à de nouvelles techniques de reconstruction [26, 27].

La reconstruction 3D donne une image très réaliste de la colonne vertébrale qui, dans de nombreux cas, est difficile à analyser de par la complexité de la forme des vertèbres. Ceci est particulièrement vrai pour la nouvelle image qui représente la colonne vertébrale en entier, vue par le haut.

Pour aider la compréhension de cette nouvelle image, pour simplifier la visualisation et pour créer une possibilité de paramétrisation mathématique, nous recommandons le remplacement des vertèbres par un vecteur regroupant toutes les caractéristiques des vertèbres (taille, orientation, rotation, etc.).

Les objectifs de la présente communication sont la présentation réelle de la colonne vertébrale en 3D fournie par EOS, la simplification de la visualisation de la colonne vertébrale à l’aide du vecteur vertébral et la comparaison des méthodes classiques de mesure de la scoliose en 2D avec le calcul des valeurs scoliotiques basé sur le vecteur vertébral. Nous voulons également montrer l’importance de la représentation dans le plan horizontal ainsi qu’une véritable analyse spatiale des résultats thérapeutiques.

MÉTHODE

Nous utilisons depuis septembre 2007 l’appareil EOS (Biospacemed, Paris, France) ainsi que son logiciel assurant une reconstruction en 3D (stérEOS, Biospacemed, Paris, France). Dans cette communication, nous analysons les données des patients ayant subi une intervention sur scoliose entre le 1er janvier et le 31 décembre 2009. La correction des courbures a été réalisée selon la philosophie de Cotrel-Dubousset en utilisant des implants SCS (Scient’X France). Les courbures pré- et postopératoires ont été analysées par un examen EOS. Les clichés préopératoires ont été réalisés entre le 7ème et le 2ème jour précédent l’intervention, les clichés postopératoires entre J+4 et J+5. Sur les clichés en 2D, dans l’analyse quantitative des courbures au plan frontal et sagittal, nous avons utilisé la méthode classique de Cobb. Dans le plan sagittal la cyphose dorsale mesurée entre Th4 et Th12 a été indiquée par un +, la lordose lombaire entre L1 et L5 par un —. Dans le plan horizontal la rotation vertébrale est calculée par le logiciel stérEOS.

La reconstruction en 3D a été réalisée par le logiciel SterEOS d’après les clichés pré- et postopératoires en 2D. Dans l’analyse des images prises par le haut, nous utilisons le concept de « vecteur vertébral » qui pourra s’adapter par la suite aux deux autres plans également.

Le « vecteur vertébral » est défini de la façon suivante : Le point de départ du vecteur vertébral est le milieu de distance interacetabulaire. (Figure 1/ a,d). Au plan sagittal le vecteur vertébral est parallèle au plateau supérieur du corps vertébral. Le point d’arrivée du vecteur est le point où le vecteur coupe le plan antérieur du corps

Fig. 1. — Définition du vecteur vertébral vertébral (Figure 1/b,e). Vu d’en haut le vecteur vertébral représente l’axe de symétrie de la vertèbre (Figure 1/c,f).

La détermination du vecteur vertébral ne dépend pas de la déformation de la vertèbre, la direction du vecteur correspond toujours à l’axe de symétrie du corps vertébral. De par sa définition la longueur du vecteur est déterminée par la taille du corps de la vertèbre, elle suit parfaitement la différence de taille des vertèbres, des cervicales aux lombaires.

Les vecteurs vertébraux peuvent être représentés dans un système de coordonnées que nous déterminons de la façon suivante : l’axe X du système est représenté par la droite reliant les points centraux des têtes fémorales. L’axe Y est perpendiculaire à l’axe X au milieu de la distance interacetabulaire et correspond à l’axe de symétrie du corps et du bassin. L’axe Z est la perpendiculaire à l’axe X et à l’axe Y au niveau du point bissecteur.

La calibration du système de coordonnées est individuelle, car la section entre le milieu de la distance interacetabulaire et le point central de la tête de l’un des fémurs correspond à 100 unités égales, quelle que soit la longueur effective de la section. La distance interacetabulaire est donc de 200 unités. Après transposition de ces unités sur les axes Y et Z, nous obtenons la calibration des trois axes (Figure 1/g).

Les dimensions et les coordonnées des vecteurs de chaque vertèbre peuvent être déterminées dans le système de coordonnées. Dans le plan horizontal sur la base des coordonnées vectorielles nous pouvons déterminer la longueur du vecteur vertébral, sa distance de l’axe médian du corps (déviation latérale de la vertèbre) et sa rotation en utilisant la tangente trigonométrique (Figure 1/h).

Nous avons comparé les valeurs angulaires horizontales et sagittales classiques, les valeurs de rotation axiale calculées par sterEOS ainsi que les valeurs angulaires en 3D calculées sur la base des vecteurs vertébraux. Les résultats ont été analysés à l’aide de Student T. Nous avons effectué une analyse de corrélation Pearson entre les valeurs mathématiques des vecteurs horizontaux des vertèbres apicales, les valeurs angulaires de Cobb et les valeurs de rotation axiale des vertèbres en cherchant les liens jouant un rôle dans la caractéristique des courbures et qui peuvent influencer le résultat de l’intervention chirurgicale.

RÉSULTATS

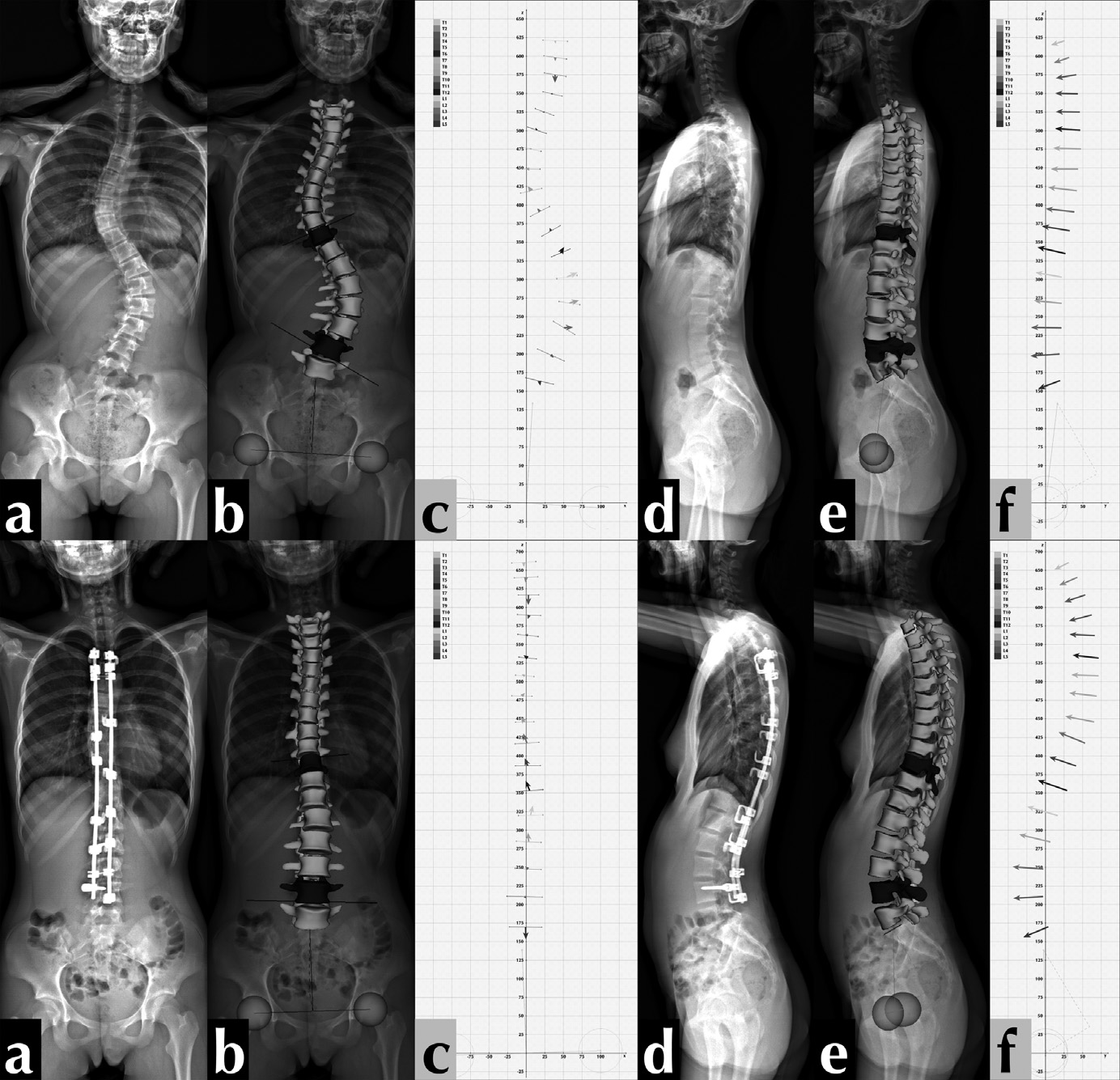
Nous avons effectué 95 interventions chirurgicales sur 87 jeunes filles et 8 garçons pour scoliose idiopathique entre le 1er janvier et le 31 décembre 2009. L’âge moyen de nos patients lors de l’intervention était de 18,6 ans (S.D :fi7,41). Des clichés de face et de profil pré- et postopératoires ont été effectués sur tous les patients (Figure 2/a,d). Nous avons effectué les reconstructions tridimensionnelles (Figure 2/b,e) ainsi que les calculs des vecteurs vertébraux (Figure 2/e,f) . Puis, nous avons visualisé par le haut les clichés 3D préopératoires (Figure 3/a) et postopératoires (Figure 3/b) et nous avons remplacé les vertèbres par les vecteurs vertébraux (Figure 3/c,d).

Fig. 2. — Les images d’EOS en 2D/3D et les vecteurs vertébraux (abcde) En moyenne nos patients souffraient d’une scoliose de 50,93°, la courbure postopé- ratoire se réduisant à 16,61° selon la méthode de mesure classique de Cobb. Les mesures effectuées d’après les vecteurs vertébraux (VV) donnèrent une scoliose préopératoire de 49,37° (VV-scoliose) et une courbure postopératoire de 16,82°. La corrélation des deux mesures angulaires était importante dans sa valeur préopératoire (r=0,950) et dans sa valeur postopératoire (r=0,935) (Tableau/lignes 1,2). De même une corrélation importante (r=0,983) a été observée au niveau de la cyphose dorsale Th4-Th12 préopératoire entre la mesure Cobb classique (25,75°) et celle calculée par les vecteurs vertébraux (VV-cyphose=28,37°), ces valeurs augmentant légèrement au cours de l’intervention (Cobb=29,21°, VV-cyphose=31,25°) (Tableau/ligne 3,4).

La lordose lombaire selon Cobb était de —43,67°, en revanche la lordose calculée par le vecteur vertébral lui était en moyenne inférieure de 8,55°. Après l’intervention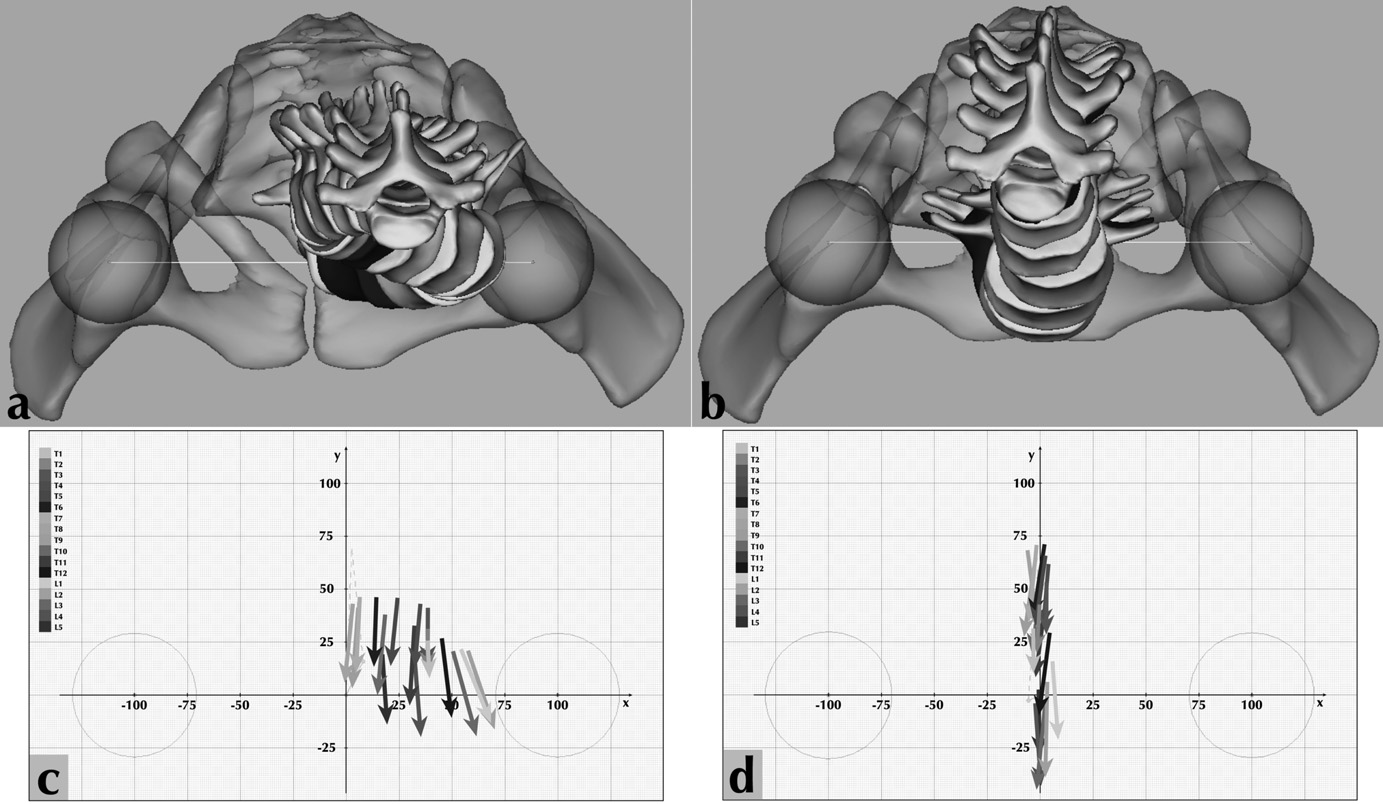

Fig. 3. — Les images vues en haut (abcd) Tableau 1 95 patients pré op post op 190 cas test T deux test T deux corrélation corrélation moyenne fi D.S.

échantillons moyenne fi D.S. échantillons Pearson Pearson appariés appariés Cobb (*) 50.93 fi18.48 -1.56*

0.950**

16.61 fi12.08 0.21† 0.935**

VV-scoliose (*) 49.37 fi20.38 16.82 fi12.85 cyphose (*) 25.75 fi17.43 2.61**

0.893**

29.21 fi9.78 2.04**

0.896**

VV-cyphose (*) 28.37 fi16.15 31.25 fi9.98 lordose (*) -43.67 fi13.4 8.55**

0.763**

-45.26 fi9.88 7.04**

0.809**

VV-lordose (*) -35.12 fi12.21 -38.22 fi9.42 RVA (*) 19.16 fi11.39 0.65*

0.963**

12.19 fi8.92 0.16† 0.968**

VA α (*) 18.51 fi12.46 12.03 fi9.03 H âge 18.67 fi7.41 18.93 fi7.40 95 patients pré op post op 190 cas moyenne fi D.S.

corrélation Pearson moyenne fi D.S.

corrélation Pearson RVA (*) 0.511**

RVA (*) 0.493**

Cobb (*) 50.93 fi18.48 VA α (*) 0.452**

16.61 (*) 0.410**

H fi12.08 VA αH VA A 0.667**

VA A 0.352**

x x VA B 0.685**

VA B 0.434**

x x ΔRVA (*) 0.195† Δ Cobb (*) 35.53 fi11.47 ΔVA α (*) 0.122† H ΔVA A 0.448**

x ΔVA B 0.480**

x ** p <0.01. * p <0.05. † p valeur non significative ; D.S. — Déviation Standard.

chirurgicale la lordose lombaire a légèrement augmenté selon les deux mesures, la différence de valeur entre les deux mesures se réduisant à 1,5° (Tableau/lignes 5,6).

La rotation des vertèbres apicales (RVA) dans le plan horizontal fut automatiquement calculée sur les clichés 3D par le software de sterEOS. La RVA préopératoire moyenne était de 19,16°, la moyenne postopératoire étant de 12,19°. Selon notre méthode basée sur les vecteur vertébraux la rotation axiale de la vertèbre apicale (VA) était de 18,51° avant l’intervention chirurgicale et de 12,03° après l’intervention. Les valeurs mesurées selon les deux méthodes montraient une forte corrélation tant dans la rotation axiale préopératoire (r=0,963) que dans la rotation axiale postopératoire (r=0,968) des vertèbres apicales (Tableau/lignes 7,8).

Dans l’analyse de la corrélation, nous pouvons montrer que la corrélation la plus forte s’observe entre l’ampleur de la scoliose et les coordonnées des points terminaux (VA B : r=0,685) et des points initiaux (VA A : r=0,667) des vecteurs verté- x x braux. Une corrélation moins étroite a été observée entre les rotations axiales (RVA:

r=0,511, VA α : r=0,452) des vertèbres et l’angle de Cobb (Tableau/ligne 9). La H correction obtenue pendant la chirurgie (Δ Cobb: 35.53°) montre aussi une étroite corrélation avec les valeurs coordonnées des points terminaux (ΔVA B : r=0.480) et x des points initiaux (ΔVA A : r=0.448) des vecteurs vertébraux. Une corrélation x moins étroite et statistiquement non significative peut être constatée entre la mesure de la correction chirurgicale (Δ Cobb) et la rotation axiale de la vertèbre apicale (ΔRVA: r=0.195, ΔVA α : r=0.122) (Tableau/ligne 10).

H DISCUSSION

Dans la scoliose idiopathique, ni l’origine, ni la nature, ni le cours de la progression de la déformation structurelle ne sont connus. Cependant la déformation première est liée à la rotation vertébrale qui provoque une instabilité dans le plan sagittal et un équilibre incertain dans le plan frontal. L’étude des composantes de la déformation tridimensionnelle nous a montré qu’il existe un lien direct et non linéaire, dont la nature n’est pas connue entre les composantes de la déformation tridimensionnelle [1]. Nous savons qu’après l’apparition de la déformation initiale, la scoliose idiopathique progresse au cours de la croissance selon un processus biomécanique autonome.

Le diagnostic clinique s’établit sur la base de clichés face et profil [7, 13, 14]. Sur la base de ces clichés en 2D de nombreuses méthodes ont été élaborées afin d’étudier la rotation axiale, mais elles se sont toutes avérées incertaines, ces clichés ne fournissant pas d’informations qualitatives ou quantitatives suffisantes quant aux structures anatomiques [16, 29].

L’appréciation la plus précise de la rotation axiale est obtenue par la TDM [17, 30].

Dans le diagnostic quotidien de la scoliose, l’utilisation de la TDM est cependant limitée par l’irradiation importante et la position couchée, la position couchée réduisant les courbures sagittales et frontales [31]. Il est également important de prendre en considération le niveau auquel nous étudions la rotation puisque dans la vertèbre, par la torsion de la vertèbre, la rotation peut-être différente au niveau du plateau supérieur ou inférieur [32]. Pour que l’image horizontale de la vertèbre soit homogène et appréciable, nous devons mesurer la rotation de la vertèbre dans un segment fixé à une distance standard de l’un des plateaux ou dans un segment représentatif de la moyenne des différences de torsion, causées par les rotations inégales des plateaux supérieur et inférieur.

Il est prouvé que la mesure de la rotation vertébrale réalisée sur la base de la reconstruction en 3D des clichés classiques donne un résultat plus précis que toutes les autres méthodes [33], d’autre part, la reconstruction en 3D permet de mesurer également la rotation intervertébrale segmentaire [34]. Cependant pour une bonne reconstruction, la définition précise de l’angle droit entre les clichés face et profil ainsi que le bon positionnement du patient sont indispensables.

L’appareil développé par Georges Charpak et le logiciel assurant la reconstruction 3D ont apporté un changement percutant dans la représentation du rachis scoliotique. L’appareil permet de réaliser simultanément en position debout des clichés face et profil avec une dose de Rx considérablement diminuée. La simultanéité des clichés réalisés dans un espace calibré évite les problèmes de positionnement qui peuvent fausser une reconstruction 3D correcte. Les images de bonne qualité permettent de définir précisément dans les plans frontal et sagittal les repères nécessaires à la reconstruction en 3D de surface, nous donnant une représentation complète du rachis dans le plan horizontal également. Ce procédé est le seul outil assurant la représentation simultanée dans les trois plans en position debout des déformations rachidiennes.

Lors de la reconstruction 3D nous obtenons des images explicitement réalistes, porteuses d’informations très détaillées. Nous avons travaillé sur l’idée de vecteur vertébral pour en faciliter la compréhension. La conception de vecteur vertébral est née sur des entités de bases exactes, bien définies, généralement approuvées et utilisées dans la nomenclature du groupe de travail de la SRS Scoliosis 3D (pediculus centroid, plateau supérieur du corps vertébral), elle s’appuie sur les notions de base de la géométrie et de la trigonométrie (perpendiculaire, droite parallèle) et utilise les éléments de l’algèbre (origine, système de coordonnées, angle).

Dans le plan frontal le vecteur vertébral a pour origine le milieu de la droite qui relie les points centraux des pédicules, dans le plan sagittal il court du plateau supérieur à la paroi antérieure du corps vertébral. Par son emplacement, il supprime les différences dues à la torsion des vertèbres puisque que dans chaque vertèbre il se situe proportionnellement à la même distance du plateau supérieur. Dans le plan horizontal il prend son origine perpendiculairement au milieu de la droite reliant les points centraux des pédicules et court dans la médiane du corps vertébral. La direction du vecteur est toujours la direction de l’axe de symétrie de la vertèbre. Par sa définition, le vecteur résume toutes les informations se rapportant à la taille, la situation, la direction de la vertèbre. Sa représentation graphique claire nous permet de mieux comprendre le processus de déformation dans l’espace.

Dans le système de coordonnées, il est possible de calculer les coordonnées des vecteurs de toutes les vertèbres, donnant ainsi une description mathématique de la situation et des forces de rotation de chaque vertèbre. Dans le diagnostic de la scoliose dans le plan frontal et sagittal, le vecteur vertébral est aussi fiable et précis que les méthodes de mesure classiques. La corrélation forte constatée entre les méthodes en est la preuve. Elle n’est pas remise en question par le fait que la lordose lombaire mesurée par le vecteur vertébral soit en moyenne inférieure à 8°. Dans la méthode Cobb le plan de mesure déterminant est le plateau inférieur de L5 alors que le vecteur vertébral est, lui, parallèle au plateau supérieur, ce qui explique que cette différence (7-10°) vient de l’angulation postérieure de L5 [35].

Dans la représentation de la troisième dimension des déformations rachidiennes, la mesure par le vecteur vertébral de la rotation de la vertèbre axiale est en parfaite corrélation avec les valeurs mesurées par le logiciel sterEOS. Compte tenu de la forte corrélation observée dans les mesures tridimensionnelles entre les méthodes classiques et le vecteur vertébral, nous pouvons affirmer que l’utilisation du vecteur vertébral nous donne pour la première fois la possibilité d’examiner simultanément les déformations rachidiennes en position debout sous la charge de la gravitation donc en position fonctionnelle.

L’utilisation du vecteur vertébral permet l’analyse simultanée de la courbure scoliotique dans le plan frontal, sagittal et horizontal. La corrélation moyennement forte entre la rotation axiale dans le plan horizontal et les valeurs angulaires dans le plan frontal signifie que, malgré le rôle primordial de la rotation axiale [28], d’autres facteurs existent dans le développement des courbures. Sur les clichés préopératoires pris par le haut, il est intéressant de constater que les vertèbres s’orientent plutôt vers l’axe × avec une rotation relativement faible. Sur la base de ces constatations, nous avons examiné la relation entre l’ampleur de la courbure et la distance avec l’axe y.

D’après nos analyses, dans le plan frontal la corrélation de la courbure scoliotique est beaucoup plus étroite avec la distance de la vertèbre à l’axe médian du corps qu’avec la rotation vertébrale.

La distance mesurée à partir de l’axe médian du corps est l’éjection latérale, exprimée par les coordonnées B du vecteur vertébral. Sur les clichés postopératoix res, les vertèbres se situent vers l’axe y. Les changements obtenus dans la courbure lors de l’intervention chirurgicale sont indéniablement en rapport avec la situation des vertèbres par rapport à l’axe médian du corps, la rotation des vertèbres ne montrant pas de corrélation très étroite. Cette conclusion semble renforcée par l’observation d’une progression dans la courbure par déviation latérale sous gravité et sans rotation axiale [36].

CONCLUSION

L’utilisation du vecteur vertébral dans l’analyse des déformations rachidiennes simplifie et facilite la compréhension du grand nombre d’informations fournies par l’appareil EOS 2D/3D. D’après l’analyse des données horizontales, le but premier des interventions correctrices serait de réduire l’éjection latérale des vertèbres, la réduction de la rotation vertébrale semblant moins importante. Ceci est un nouvel élément dans l’approche de la thérapie des déformations rachidiennes qui demande naturellement à être plus étudié.

BIBLIOGRAPHIE [1] Panjabi M.M., White A.A. — Basic biomechanics of spine.

Neurosurgery, 1980, 7, 76-93.

[2] Vrtovec T., Pernus F., Likar B. — A review of methods for quantitave evaluation of axial vertebral rotation. Eur. Spine J., 2009, 18, 1079-1090.

[3] Greenspan A., Pugh J., Norman A., Norman R. — Scoliotic index : a comparative evaluation of methods for the measurement of scoliosis. B. Hosp. Jt. Dis. Ort. , 1978, 39 , 117-125.

[4] Diab K., Sevastik J., Hedlung R., Suliman I. — Accuracy and applicability of measurement of the scoliotic angle at the frontal plane by Cobb’s method, by Ferguson’s method and by a new method. Eur. Spine J. , 1995, 4, 291-295.

[5] Chen Y.L., Chen W.J., Chiou W.K. — An alternative method for measuring scoliosis curvature. Orthopedics, 2007, 30, 828-831.

[6] Ferguson A. — The study and treatment of scoliosis.

South Med. J. , 1930, 23 , 116-120.

[7] Cobb J. — Outline for the study of scoliosis.

Am. Acad. Orthop. Surg. Instr. Course Lect., 1948, 5, 261-275.

[8] Harrison D.E., Cailliet R., Harrison D.D., Janik T., Holland B. — Reliability of centroid, Cobb, and Harrison posterior tangent methods: which to choose for analysis of thoracic kyphosis. Spine, 2001, 26 , E227-E234.

[9] Polly D., Killkelly F., McHale K., Asplund L., Mulligan M., Chang A. — Measurement of lumbar lordosis : evaluation of intraobserver, interobserver, and technique variability.

Spine , 1996, 21 , 1530-1535.

[10] Stotts A., Smith J., Santora S., Roach J., D’Astous J. — Measurement of spinal kyphosis :

implications for the management of Scheuermann’s kyphosis. Spine , 2002, 27 , 2143-2146.

[11] Hicks G., George S., Nevitt M., Cauley J., Vogt M. — Measurement of lumbar lordosis :

inter-rater reliability, minimum detectable change and longitudinal variation. J. Spinal Disord., 2006, 19, 501-506.

[12] Mac-Thiong J.M., Labelle H., Charlebois M., Huot M.P., De Guise J. — Sagittal plane analysis of the spine and pelvis in adolescent idiopathic scoliosis according to the coronal curve type. Spine , 2003, 28 , 1404-1409.

[13] Nash C., Moe J. — A study of vertebral rotation.

J. Bone Joint Surg. , 1969, 51A , 223.

[14] Perdroille R., Vidal J. — Morphology of scoliosis: three-dimensional evolution.

Orthopae- dics , 1987, 10 , 909-915.

[15] Mehta M.H. — Radiographic estimation of vertebral rotation in scoliosis.

J. Bone Joint Surg.

Br. , 1973, 55Br , 513-520.

[16] Omeroglu H., Ozekin O., Bicimoglu A. — Measurement of vertebral rotation in idiopathic scoliosis using the Perdriolle torsiometer : a clinical study on intraobserver and interobserver error. Eur. Spine J. , 1996, 5 , 167-171.

[17] Aaro S., Dahlborn M. — Estimation of vertebral rotation and spine rib cage deformity in scoliosis by computer tomography. Spine , 1981, 6, 460-467.

[18] Krismer M., Chen A.M., Steinlecher M. et al . — Measurement of vertebral rotation : a comparison of two methods based on CT scans.

J. Spinal. Disord. , 1999, 12 , 126-130.

[19] Gocen S., Aksu M.G., Baktiroglu L. et al. — Evaluation of computer tomographic methods to measure vertebral rotation in adolescent idiopathic scoliosis : an intraobserver and interobserver analysis. J. Spinal. Disord. , 1998, 11 , 210-214.

[20] Stokes I.A.F. — Three-dimensional terminology of spinal deformity. A report presented to Scoliosis Research Society by the Scoliosis Research Society Working Group on 3-D terminology of spinal deformity. Spine, 1994, 19, 236-248.

http://nobelprize.org/nobel_prizes/physics/laureates/1992/press.html.

[21] Charpak G. — La detection des particules. Recherche , 1981, 128, 1384-1396.

[22] Charpak G — Electronic imaging of ionizing radiation with limited avalanches in gases.

Rev.

Mod. Phys., 1993, 65 , 591-598.

[23] Kalifa G., Charpak G., Maccia C., Fery-Lemonnier E., Bloch J., Bboussard J.M., Attal M., Dubousset J., Adamsbaum C. — Evaluation of a new low-dose digital x-ray device : first dosimertric and clinical result in children. Pediatr. Radiol., 1998, 28 , 557-561.

[24] Dubousset J., Charpak G., Dorion I., Skalli W., Lavaste F., De Guise J.A., Kalifa G., Ferey S. — Le system EOS. Nouvelle Imagerie Osteo-Articulaire basse dose en position debout. e-mémoire de l’Académie National de Chirugie, 2005, 4 , 22-27.

[25] Dubousset J., Charpak G., Dorion I., Skalli W., Lavaste F., De Guise J.A., Kalifa G., Ferey S. — A new 2D and 3D imaging approach to musculosceletal physiology and pathology with low-dose radiation and the standing position: the EOS sytem. Bull. Acad. Natl.. Med. , 2005, 189 , 287-297.

[26] Le Bras A., Laporte S., Mitton D., De Guise J.A., Skalli W. — 3D detailed reconstruction of vertebrae with low dose digital stereoradiography. Stud Health Technol. Inform. , 2002, 91 , 286-290.

[27] Le Bras A., Laporte S., Mitton D., De Guise J.A., Skalli W — A biplanar reconstruction method based on 2D and 3D contours: application to the distal femur. Comput. Methods Biomech. Biomed. Engin. , 2003, 6 , 1-6.

[28] Roaf R. — Rotation mouvements of the spine with special reference to scoliosis.

J Bone Joint

Surg. [Br], 1958, 40 , 312-332.

[29] Skalli W., Lavaste F., Descrimes J.L. — Quantification of three-dimensional vertebral rotations in scoliosis ;: what are the thrue values. Spine , 1995, 20 , 546-553.

[30] Ho E.K.W., Upadlyay S.S., Chan F.L. et al . — New method of measuring vertebral rotation from computed tomographic scans.

Spine , 1993, 18 , 1173-1177.

[31] Yazici M., Acaroglu E.R., Alanay A., Deviren V., Cila A., Surat A. — Measurement of vertebral rotation in standing versus supine position in adolescent idiopathic scoliosis. J.

Pediatr. Orthop., 2001, 21, 252-256.

[32] Dubousset J. — Three-Dimensional Analysis of the Scoliotic Deformity. in The Pediatric

Spine: Principles and Practice, 1994, ed. WeinsteinSL Raven Press Ltd., New York, pp. 479-496.

[33] Gille O., Champain N., Benchikh-el-Fegoun A., Vital J.M., Skalli W. — Reliability of the spine of milde scoliotic patents. Spine, 2007, 32, 568-573.

[34] Dumas R., Steib J.P., Mitton D., Lavaste F., Skalli W. — Three-dimensional quantitative segmental analysis of scoliosis corrected by the in situ contouring technique Spine , 2003, 28 , 1158-1162.

[35] Masharawi Y., Salame K., Mirovsky Y., Peleg S., Dar G., Steinberg N., Hershkovitz I.

— Vertebral body shape variation in the thoracic and lumbar spine : characterization of its asymmetry and wedging. Clin. Anat. , 2008, 21 , 46-54.

[36] Drevelle X., Lafon Y., Ebermeyer E., Courtois I., Dubousset J., Skalli W. — Analysis of idiopathic scoliosis progression by using numerical simulation. Spine , 2010, 35 , E407-12.

DISCUSSION

M. Jean DUBOUSSET

Vous n’avez peut-être pas assez insisté sur l’apport considérable qui ressort de votre présentation à savoir une mesure enfin exacte de la déformation dans le plan horizontal, ce que ne donnait pas la mesure de l’angle de Cobb et même des mesures de la rotation axiale.

Pensez-vous qu’avec le système des vecteurs on puisse déceler le démarrage des dislocations vertébrales du rachis dégénératif qui commence souvent en L3 L4 et qui ne sont décelées que souvent tardivement ?

Effectivement, le vecteur vertébral change radicalement notre mode de pensée sur la scoliose. C’est surtout vrai en ce qui concerne le plan horizontal. La dégénération discale qui est signe précoce de la scoliose dégénérative lombaire provoque une instabilité vertébrale qui est visible, non seulement dans la rotation pathologique, mais également dans la dislocation latérale de la vertèbre : je pense donc que le vecteur vertébral est une aide sérieuse dans le diagnostic précoce des scolioses lombaires dégénératives chez le sujet âgé, puisque dans les clichés horizontaux une rotation minimale ou l’apparition d’une éjection latérale est un signe prémonitoire de pathologie dégénérative et de scoliose.

M. Jean-Daniel SRAER

Comment pouvez-vous rétablir une colonne dont la stature est normale, à partir de telles lésions vertébrales ?

La correction des déformations vertébrales a été radicalement changée par l’introduction d’une nouvelle philosophie et d’une nouvelle technique en 3D. L’élaboration de cette correction en 3D est intimement liée au nom du Professeur Dubousset et la philosophie qui l’accompagne, reconnue dans le monde entier, représente le fondement de toutes les techniques 3D actuelles. J’ai moi-même intégré cette philosophie de la correction spatiale de la scoliose auprès du Professeur Dubousset à l’occasion d’une bourse française. J’ai utilisé cette technique étudiée en France pour tous les cas présentés ici même dans la planification et la réalisation des interventions.

M. Emmanuel-Alain CABANIS

Établissez-vous une corrélation mathématique désormais simple à réaliser (avant et après) entre correction chirurgicale et gain de la stature ?

Le système de coordonnées utilisé pour déterminer le vecteur vertébral nous donne la possibilité de déterminer les cordonnées du vecteur dans les trois plans de l’espace. Sur la base de ces coordonnées, en utilisant de simples rapports angulaires dans les plans frontal, sagittal et horizontal, nous pouvons déterminer la longueur de la colonne. Sur ces bases, il est facile de calculer à partir des données initiales et en cas de correction totale, l’augmentation espérée de la taille. Comme il est difficile d’obtenir une correction de 100 %, l’augmentation réelle de la taille est toujours moindre que celle calculée sur la base des coordonnées vectorielles. Nous travaillons actuellement à élaborer un algorithme de calcul qui sera le plus simple possible.

M. Jacques BATTIN

Dans la maladie de Marfan on observe des scolioses majeures, mais on en a la pathogenèse, la laminopathie expliquant les autres anomalies aortiques et oculaires. Mais dans les scolioses idiopathiques, quelle cause invoquer ?

La scoliose idiopathique est une maladie génétique, cela semble prouvé par des examens effectués sur des jumeaux. En revanche, la question de savoir si l’apparition de la maladie est due à la déficience d’un gène majeur ou de plusieurs gènes n’est pas encore élucidée.

D’après de nombreux travaux effectués récemment, il semblerait que la scoliose idiopathique est une maladie polygénique multifactorielle à expression et pénétrance variables.

Nous supposons que la cause de la maladie est la déficience conjointe de plusieurs gènes, dont les gènes de la mélatonine, de la leptine, de la bone morphogenetic protein et de la metalloproteinase. Parallèlement à ces déficiences génétiques, des facteurs environnementaux inconnus ont également un rôle important dans l’apparition de la maladie.

M. Bernard SALLE

Le pronostic de la scoliose chez l’enfant dépend-il aussi de l’étiologie ? Je pense aux hernies diaphragmatiques qui opérées sont suivies d’une scoliose comme complication de la chirurgie.

Bien sûr, le pronostic de la scoliose dépend de son étiologie, de l’âge et du potentiel de croissance du patient. En général le pronostic des scolioses dont l’étiologie est connue est moins bon que dans les cas de scoliose idiopathique. Certaines malformations congénitales des vertèbres qui restent intraitées peuvent provoquer de graves déformations, de même que les déformations liées aux pathologies neuromusculaires et aux maladies systémiques. Les scolioses apparaissant avant l’âge de six ans forment le groupe des « early onset scoliosis » et provoquent donc des déformations très importantes jusqu’à la fin de la croissance. Les scolioses idiopathiques apparaissent en général au début de la puberté et nous les appelons les « late onset scoliosis ». Leur progression est plus lente que dans les formes apparaissant précocement. Dans ce cadre, il est vrai que les enfants subissant une thoracotomie précoce, souffrent toujours postérieurement d’une scoliose.

Bull. Acad. Natle Méd., 2011, 195, no 3, 629-643, séance du 1er mars 2011