INTRODUCTION

Les maladies cardiovasculaires sont responsables en Europe de plus de quatre millions de décès chaque année, soit près de la moitié des décès non accidentels [1].

Il s’agit essentiellement des conséquences de maladies telles que les maladies coronariennes, l’insuffisance cardiaque, et les arythmies cardiaques. Or, la détection précoce de ces maladies, l’évaluation de leur gravité, la prédiction de leur évolution et de l’effet des thérapies sont des éléments essentiels pour améliorer la prise en charge des patients et pour réduire de façon significative la mortalité et la morbidité.

Pour établir le diagnostic, plusieurs modalités d’imagerie cardiaque permettent d’observer le fonctionnement du cœur. Ce sont notamment l’imagerie par résonance magnétique (IRM), la tomodensitométrie par rayons X, l’échocardiographie, l’imagerie de médecine nucléaire (scintigraphies), qui fournissent des informations anatomiques et fonctionnelles dynamiques sur l’organe. Des signaux complémentaires d’électrophysiologie mesurent des potentiels électriques à la surface du thorax ou par voie endovasculaire à la surface de l’endocarde d’un ventricule ou d’une oreillette. D’autres signaux biologiques peuvent être mesurés, notamment hémodynamiques comme des pressions ou des flux sanguins.

La quantité et la diversité de ces informations rendent leur analyse très difficile. Les signaux d’imagerie sont généralement 4D, incluant trois dimensions spatiales et une dimension temporelle. Les signaux d’électrophysiologie sont également multidimensionnels. Cette complexité rend très difficiles la quantification précise de la pathologie, la prédiction de son évolution et le bénéfice attendu d’un choix thérapeutique. Par exemple, entre 30 et 40 % des patients auxquels on implante un stimulateur cardiaque pour une resynchronisation cardiaque biventriculaire ne répondent pas au traitement [2, 3].

Pour améliorer cette situation, une stratégie prometteuse consiste à intégrer les informations provenant de l’imagerie et de l’électrophysiologie dans des modèles numériques capables de décrire et de simuler l’activité électrique, mécanique et hémodynamique du cœur [4-6]. Cette stratégie offre plusieurs avantages majeurs, notamment :

• la capacité d’intégrer de façon unifiée des mesures hétérogènes (images anatomiques et fonctionnelles, signaux électriques et hémodynamiques, etc.), • la capacité de fournir des mesures quantitatives et objectives liées à la fonction cardiaque et à la viabilité de l’organe, • la capacité de simuler l’évolution d’une pathologie ou les effets d’une thérapie.

Dans cet article, nous illustrons cette stratégie en présentant la construction d’un modèle numérique personnalisé biventriculaire du cœur. Nous présentons d’abord la modélisation géométrique du cœur à partir d’images anatomiques et fonctionnelles, puis la modélisation des composantes électrique, mécanique et hémodynamique.

Nous illustrons l’utilisation du modèle personnalisé pour la planification de deux types d’interventions (ablation radiofréquence et resynchronisation cardiaque) avant de conclure sur les défis scientifiques qu’il convient de relever avant de transposer ces outils dans la pratique clinique courante.

LE MODÈLE ANATOMIQUE

Le premier niveau de modélisation du cœur numérique personnalisé est géométrique. On commence par appliquer des logiciels de segmentation des images anatomiques et fonctionnelles du patient pour extraire les principales régions d’intérêt de l’organe : les oreillettes, les ventricules, les cavités, les valves, les piliers, etc. Des efforts de recherche importants en analyse d’images au cours des quinze dernières années [7-12] ont permis d’automatiser presque totalement cette étape [13, 14].

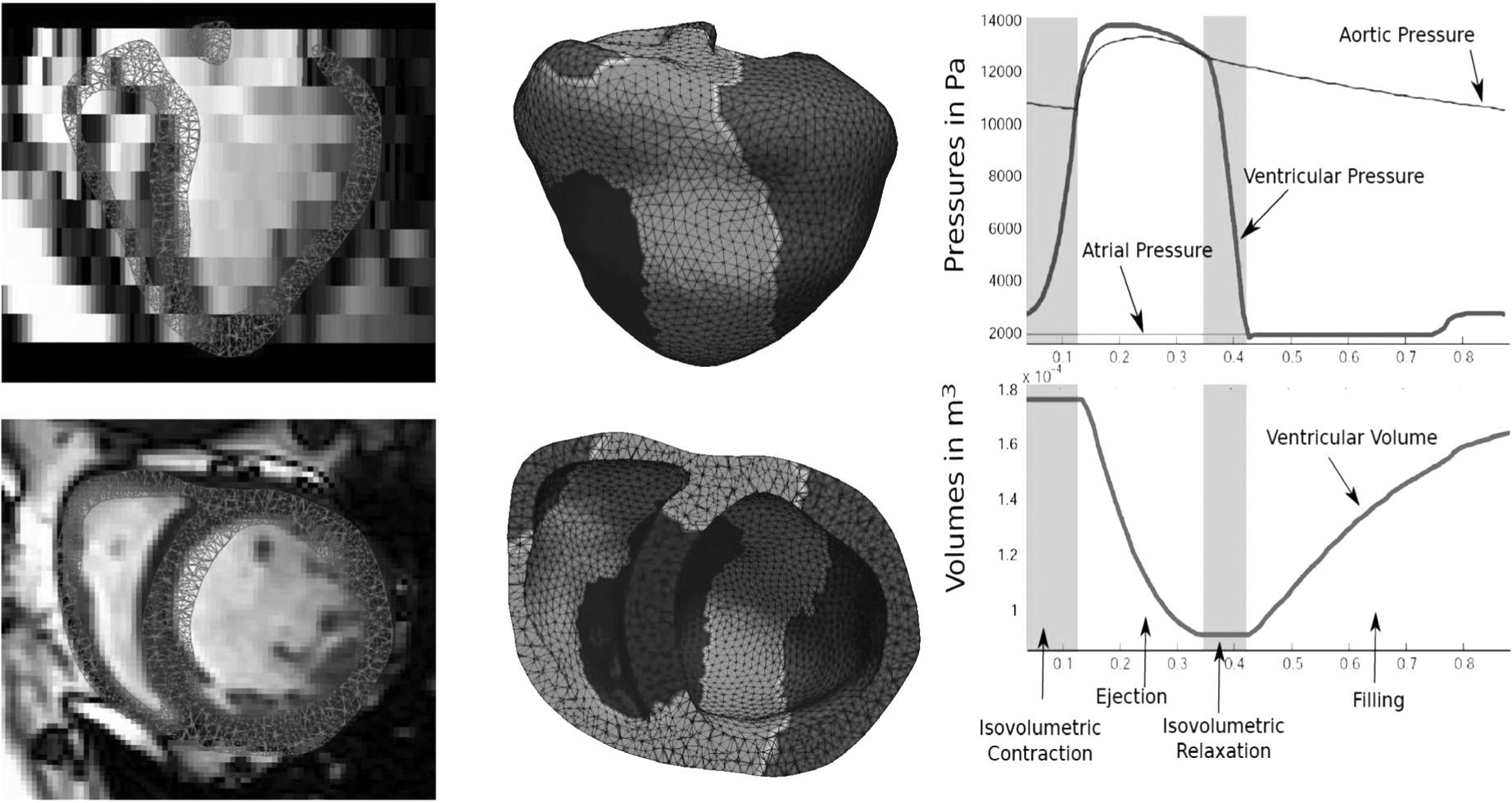
On construit ensuite pour chaque région extraite un maillage formé généralement d’un grand nombre de tétraèdres (typiquement de plusieurs dizaines de milliers jusqu’à plusieurs millions). Chaque tétraèdre couvre un petit élément de volume de l’organe et contient des informations sur la région anatomique concernée, ainsi que sur les propriétés biophysiques du tissu à l’endroit considéré. Celles-ci proviennent en partie des images anatomiques et fonctionnelles du patient considéré (par exemple les cicatrices sont révélées par l’IRM à rehaussement tardif de contraste), et en partie d’atlas anatomiques qui contiennent des informations statistiques acquises sur une population de sujets comparables (Figure 1).

Il est notamment important de connaître la direction des principaux faisceaux de fibres cardiaques qui jouent un rôle essentiel dans la propagation de l’onde électrique et dans l’activité mécanique de l’organe. Si des recherches récentes très prometteuses [15] permettent d’acquérir cette information à travers l’IRM de diffusion sur le cœur battant d’un patient spécifique, cette technique n’est pas encore utilisable dans la pratique clinique courante. C’est pourquoi nous avons construit un atlas moyen des fibres cardiaques à partir des IRM de diffusion de cœurs fixés postmortem [16, 17]. Cet atlas est ensuite déformé pour adopter la forme précise du cœur du patient considéré, et fournir ainsi en chaque point du myocarde une prédiction raisonnable de la direction des faisceaux de fibres cardiaques (Figure 2).

LE MODÈLE ÉLECTRIQUE

Le second niveau de modélisation est électrique, il est construit sur le modèle géométrique précédent. Il s’agit de décrire le phénomène de propagation de l’onde

Fig. 1. — Construction d’un maillage tétraédrique 3-D à partir des images cardiaques volumiques.

Fig. 2. — Modélisation de la structure des principaux faisceaux de fibres cardiaques à partir de l’imagerie de diffusion.

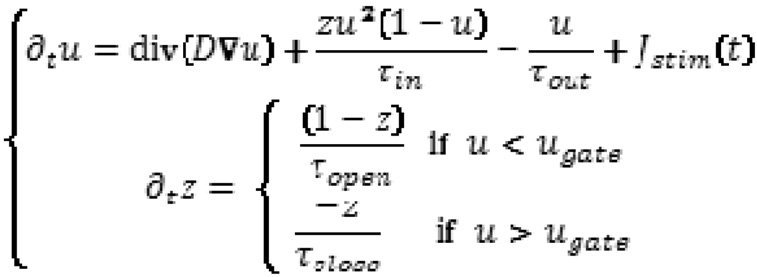
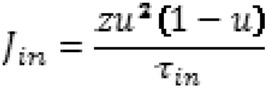du potentiel électrique transmembranaire dans les tissus cardiaques, et notamment la dépolarisation des deux ventricules suivie de leur repolarisation.

Il existe de nombreux modèles décrivant l’activité électrique du cœur, depuis les travaux pionniers de Denis Noble [18] et les recherches au sein du projet Physiome [19]. Un état de l’art récent est publié par [20]. Les modèles choisis doivent être compatibles avec les échelles d’observation macroscopique du cœur en clinique.

C’est pourquoi nous avons considéré des modèles phénoménologiques qui décrivent avec des équations aux dérivées partielles l’évolution d’un potentiel d’action dans chaque élément de volume. Ce potentiel d’action correspond au potentiel transmembranaire moyen des cellules cardiaques dans un élément de volume.

Dans cette catégorie de modèles, celui de Mitchell et Schaeffer [21] est un modèle à deux variables qui décrit le potentiel transmembranaire ou potentiel d’action comme la somme d’un courant diffusif passif et de plusieurs courants réactifs actifs incluant un courant ionique sodium et calcium rapide (entrant) et un courant ionique potassium lent (sortant). Il est décrit par le système suivant d’équations aux dérivées partielles :

où u est la variable décrivant le potentiel d’action normalisé, et z une variable liée au courant des ions sodium et calcium et contrôlant les phases d’ouverture et fermeture des canaux ioniques déclenchant ainsi les phases de dépolarisation et repolarisation.

représente le courant ionique sodium et calcium entrant et rapide qui fait croître le potentiel d’action (dépolarisation) et représente le courant ionique potassium sortant et lent qui fait décroitre le potentiel d’action (repolarisation).

est le courant de stimulation lié à l’électrode de stimulation.

Le terme de diffusion fait intervenir un tenseur D anisotrope qui est lié à la direction des fibres cardiaques, et qui est personnalisé dans le modèle géométrique grâce à l’IRM de diffusion.

Un tel modèle, permet de simuler de façon réaliste certains aspects macroscopiques de l’électrophysiologie cardiaque sur des maillages de plusieurs millions de tétraè- dres. Sa personnalisation est obtenue en comparant les temps de passage de l’onde électrique simulée et de l’onde mesurée, et en cherchant à les faire coïncider au mieux. Cette personnalisation est facilitée par le fait qu’il est possible d’identifier à partir des mesures et de façon indépendante un paramètre lié à la conductivité apparente et un paramètre lié à la durée du potentiel d’action. On peut également identifier les paramètres de la fonction liant la durée du potentiel d’action à la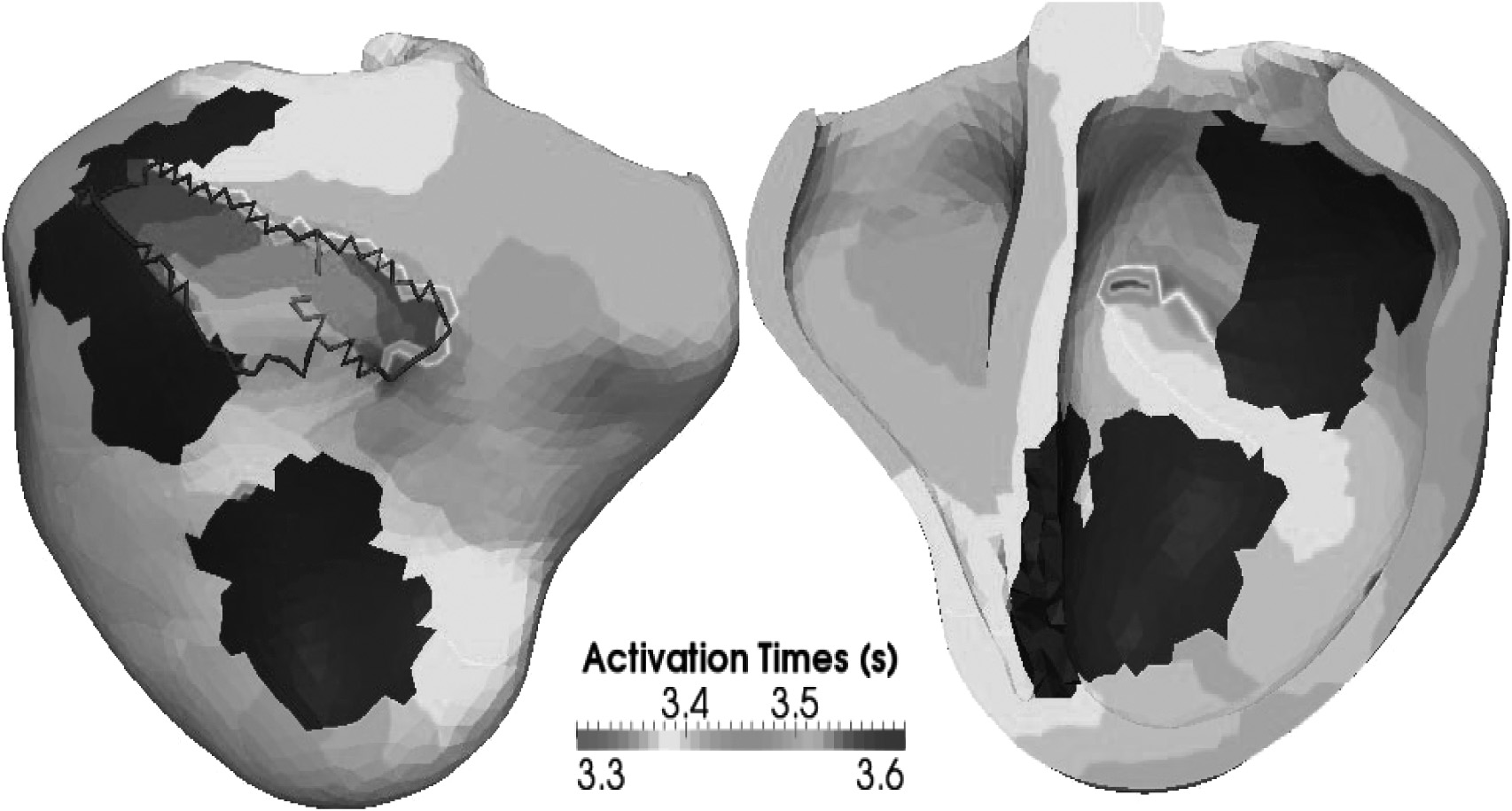 fréquence cardiaque (courbes de restitution), une information très importante pour simuler l’induction de tachycardies ventriculaires.

En prenant en compte l’anisotropie de conductivité due aux fibres cardiaques et l’hétérogénéité de conductivité due notamment à la présence de cicatrices (zones ischémiques, nécrosées, fibroses), il est possible de faire apparaître (Figure 3) pour certaines fréquences de stimulation des courants de réentrée et des blocs de conductivité qui peuvent entraîner une tachycardie ventriculaire aux conséquences potentiellement fatales (fibrillation et mort subite) [22, 23]. Grâce à la simulation on peut aussi évaluer un risque local d’induction de tachycardie ventriculaire, guider la position des sondes d’un stimulateur cardiaque, décider de l’implantation d’un défibrillateur associé, ou planifier et simuler un protocole d’ablation radiofréquence de régions spécifiques du myocarde [24].

Fig. 3. — Simulation de l’électrophysiologie du cœur numérique personnalisé permettant de révéler des circuits de réentrée autours de cicatrices cardiaques.

LE MODÈLE MÉCANIQUE

Le troisième niveau est mécanique et il est construit sur les modèles géométriques et électriques précédents. Il s’agit de traduire le passage de l’onde électrique en une contraction des fibres cardiaques.

Le cœur est un matériau complexe, à la fois actif, non linéaire, viscoélastique, anisotrope et incompressible. Nous avons choisi un modèle développé à l’Inria par les équipes de M. Sorine [25] puis D. Chapelle [26, 27] et inspiré par les travaux pionniers de Hill et Maxwell. Ce modèle est macroscopique mais s’appuie sur une analyse multi-échelle, depuis les moteurs ATP à l’échelle nanoscopique, jusqu’aux sarcomères à l’échelle microscopique, aux fibres cardiaques à une échelle mésosco- pique et enfin aux tissus du myocarde, voire du cœur entier, à une échelle macroscopique.

Dans ce modèle on considère à nouveau des équations aux dérivées partielles dans lesquelles u est le potentiel d’action du modèle électrique précédent, et où kc, èc, τ c et ko sont respectivement la raideur équivalente, le taux de déformation, la contrainte active et la raideur maximale du sarcomère, σ c est la contrainte totale et σ o la valeur maximale de la contrainte active.

Ces équations différentielles, éventuellement simplifiées [28] sont résolues sur le maillage géométrique des ventricules en imposant des conditions aux limites qui prennent en compte les principales phases du cycle cardiaque. Lorsque les valves cardiaques sont fermées, on impose une contrainte d’incompressibilité des cavités, tandis que lorsque celles-ci sont ouvertes, on impose une condition de pression exercée par le fluide sanguin sur la paroi des cavités cardiaques, intégrant la compliance des artères et la résistance de la post-charge.

Ce modèle peut être raffiné pour prendre en compte une approximation de l’écoulement du sang dans les ventricules et dans les vaisseaux proches (notamment la crosse aortique) et il permet de reproduire avec réalisme le mouvement de contraction et de torsion du cœur. La nature biophysique du modèle permet d’évaluer des paramètres physiologiques importants comme les courbes de pression et volume des ventricules ainsi que des mesures locales de contractilité et de pression.

La personnalisation des paramètres mécaniques est obtenue en comparant le mouvement simulé et le mouvement observé dans les images cardiaques. C’est un problème difficile car le nombre de paramètres mécaniques augmente très rapidement si on autorise leur variation spatiale, ce qui est souhaitable pour détecter des pathologies. Des stratégies prometteuses consistent à estimer de façon hiérarchique les paramètres mécaniques supposés constants sur des territoires vasculaires de plus en plus fin. Des résultats encourageants sont obtenus par des approches d’assimilation de données variationnelles [29] ou séquentielles [30].

La Figure 4 présente un exemple de personnalisation électrique et mécanique du cœur d’une patiente souffrant d’insuffisance cardiaque avec un bloc de branche gauche et des zones de fibroses. Ce cœur numérique ainsi personnalisé a permis de simuler différents protocoles de resynchronisation cardiaque et de prédire quantitativement l’amélioration de la fonction cardiaque en fonction de la position des sondes et des délais imposés entre les signaux de resynchronisation. Lorsque cette approche sera validée sur un nombre suffisant de patients, on pourra envisager de l’utiliser pour sélectionner les patients les plus à même de bénéficier d’une thérapie de resynchronisation cardiaque, et d’optimiser par la simulation les paramètres et la localisation des sondes implantées sur ces patients [31, 32].

Fig. 4. — Simulation de l’activité électromécanique du cœur numérique personnalisé d’une patiente souffrant d’un bloc de branche gauche, permettant de quantifier la fonction cardiaque et de planifier une resynchronisation cardiaque.

CONCLUSION ET PERSPECTIVES : du cœur au corps numérique

La modélisation informatique et mathématique permet de construire à partir des images et des signaux cardiaques un modèle numérique et personnalisé du cœur du patient. Ce modèle, encore imparfait, permet déjà de quantifier des aspects importants de la fonction cardiaque, et de prédire l’effet de certaines thérapies par la simulation.

Il reste cependant de nombreux défis scientifiques à relever pour parvenir à une pratique clinique courante.

Il faudra notamment introduire • des mesures moins invasives pour la personnalisation du modèle, remplaçant la mesure de potentiels électriques dans les ventricules par des mesures acquises sur le thorax du patient (ECG, VCG, cartes de potentiels thoraciques) [33] ;

• une simulation plus fine de la mécanique des fluides sanguins [34], qui peut bénéficier de techniques modernes d’imagerie comme l’IRM à contraste de phase ;

• une modélisation et une simulation plus fines de diverses formes de thérapie (resynchronisation cardiaque, ablation radiofréquence, chirurgie, pose de valves, etc.) [35] ;

• la simulation du remodelage du cœur après une thérapie et la modélisation du développement du cœur chez l’enfant [36] ;

• la prise en compte des incertitudes de mesure et de modélisation [37] ;

• des mesures microscopiques in vivo des tissus cardiaques [38] ;

• l’exploitation de très grandes bases de données cardiaques [39] et de méthodes modernes d’apprentissage en informatique.

Ces perspectives s’inscrivent plus largement dans le cadre du développement du patient numérique personnalisé [40] au service d’une médecine personnalisée, plus préventive et plus prédictive.

REMERCIEMENTS

Les auteurs tiennent à remercier tout particulièrement à l’Inria l’ensemble des membres de l’équipe Asclepios (notamment S. Marchesseau et J. Relan) ainsi que leurs collègues M. Sorine, D. Chapelle et JF. Gerbeau et les membres de leurs équipes Sisyphe, Macs et Reo. Les auteurs tiennent à remercier tous leurs partenaires académiques extérieurs (notamment l’équipe Creatis à Lyon), tous leurs partenaires cliniques (notamment le Pr. R. Razavi (KCL, Londres) et le Pr. M. Haïssaguerre (IHU Lyric, Bordeaux) et leur équipes respectives, ainsi que le Dr. E. Saloux à Caen), et tous leurs partenaires industriels (notamment General Electric, Philips et Siemens).

BIBLIOGRAPHIE [1] Leal J., Luengo-Fernandez R., Gray A., Petersen S., and Rayner M. — Economic burden of cardiovascular diseases in the enlarged European Union. Eur. Heart. J. , 2006, 27(13) , 1610-9.

[2] Niti R. Aggarwal, Matthew W. Martinez, Bernard J. Gersh & Panithaya Chareonthaitawee. — Role of cardiac MRI and nuclear imaging in cardiac resynchronization therapy.

Nature Reviews Cardiology , Décembre 2009, 6 , 759-770.

[3] S. Adam Strickberger, Jamie Conti, Emile G. Daoud, Edward Havranek, Mandeep R.

Mehra, Ileana L. Pin˜a, MD, James Young. — Patient Selection for Cardiac Resynchronization Therapy. Circulation . 2005, 111 , 2146-2150.

[4] Ayache N., editor. — Computational Models for the Human Body, Handbook of Numerical Analysis (Ph. Ciarlet series editor). Elsevier, 2004, 670 pp.

[5] Ayache N., Boissel J.P., Brunak S., Clapworthy G., Lonsdale G., Fingberg J., Frangi A., Deco G., Hunter P., Nielsen P., Halstead M., Hose R., Magnin I., Martin-Sanchez F., Sloot P., Kaandorp J., Hoekstra A., Vansint Jan S., Viceconti M. — Towards Virtual Physiological Human (VPH), European White Paper, edited by DG INFSO & DG JRC, Nov.

2005.

[6] Smith N., Vecchi A. De, McCormick M., Nordsltten D., Camara O., Frangi A.F., Delingette H., Sermesant M., Relan J., Ayache N., Krieger M.W., Schulze W., Hose R., Valverde I., Beerbaum P., Staicu C., Siebes M., Spaan J., Hunter P., Weese J., Lehmann H., Chapelle D., and Razavi R. — Heart : Personalized and integrated cardiac care using patient-specific cardiovascular modelling. Journal of the Royal Society Interface Focus , 2011, 1(3) , 349-364.

[7] Ayache N. editor. — First international conference on computer vision, virtual reality and robotics in medicine, CVRMed’95, volume 905 of Lecture Notes in Computer Science, Nice, France, April 1995. Springer.

[8] Duncan J. and Ayache N. — Medical Image Analysis : Progress over two decades and the challenges ahead. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2000, 22(1) , 85-106.

[9] Ayache N. and Delingette H. editors. — Proceedings of the International Symposium on Surgery Simulation and Soft Tissue Modeling, volume 2673 of Lecture Notes in Computer

Science , Juan-les-Pins, France, June 2003. Springer.

[10] Ayache N., Ourselin S., and Maeder A., editors. — Medical Image Computing and Computer-Assisted Intervention — MICCAI 2007 — Part I, volume 4791 of LNCS, Brisbane, Australia, October 2007. Springer. Note : 1001 pp.

[11] Ayache N., Delingette H., and Sermesant M. editors. — Functional Imaging and Modeling of the Heart — FIMH 2009, volume 5528 of LNCS, Nice, France, June 2009. Springer. Note, 537 pp.

[12] Ayache N., Clatz O., Delingette H., Malandain G., Pennec X., and Sermesant M. — Asclepios : a Research Project-Team at INRIA for the Analysis and Simulation of Biomedical Images. In Bertot Y., Huet G., Lévy J.-J., and Plotkin G., editors, From semantics to computer science : essays in honor of Gilles Kahn, pages 415-436. Cambridge University Press, 2009.

[13] Peters J., Ecabert O., Meyer C., Kneser R., Weese J. — Optimizing boundary detection via Simulated Search with applications to multi-modal heart segmentation. Medical Image Analysis , February 2010, Vol. 14 , Issue 1.

[14] Ionasec R.I., Voigt I., Georgescu B., Yang Wang, Houle H., Vega-Higuera F., Navab N., Comaniciu D. — Patient-Specific Modeling and Quantification of the Aortic and Mitral Valves From 4-D Cardiac CT and TEE. Medical Imaging, IEEE Transactions on , Sept. 2010, vol. 29 , no. 9, pp. 1636-1651.

[15] Toussaint N., Stoeck C.T., Kozerke S., Sermesant M., and Philip G. — Batchelor. In-vivo Human 3D Cardiac Fibre Architecture : Reconstruction Using Curvilinear Interpolation of Diffusion Tensor Images. In MICCAI’10, LNCS, 2010. Springer.

[16] Lombaert H., Peyrat J.M., Croisille P., Rapacchi S., Fanton L., Clarysse P., Delingette H., and Ayache N. — Statistical Analysis of the Human Cardiac Fiber Architecture from DT-MRI. In Leon Axel and Dimitris Metaxas, editors, Proceedings of FIMH Conference 2011, volume 6666 of LNCS, May 2011. Springer, 171-179 pp.

[17] Peyrat J-M, Sermesant M., Pennec X., Delingette H., Xu C., McVeigh E. R., and Ayache N. — A Computational Framework for the Statistical Analysis of Cardiac Diffusion Tensors:

Application to a Small Database of Canine Hearts. IEEE Transactions on Medical Imaging ,

November 2007, 26(11) , 1500-1514.

[18] Noble D. — Modeling the Heart — from Genes to Cells to the Whole Organ.

Science , 1 March 2002,

Vol. 295 , no. 5560, 1678-1682 pp.

[19] P.J. Hunter and T.K. Borg. — Integration from Proteins to Organs : The Physiome Project.

Nature , 2003, 4 , 3(237-243).

[20] Clayton R.H., Panfilov A.V. — A guide to modelling cardiac electrical activity in anatomically detailed ventricles. Progress in Biophysics and Molecular Biology , January-April 2008, Vol.

96 , Issues 1-3, 19-43 pp.

[21] Colleen C. Mitchell, David G. Schaeffer. — A two-current model for the dynamics of cardiac membrane, 2003. Bulletin of Mathematical Biology , 65 , (5), 767-793.

[22] Relan J., Chinchapatnam P., Sermesant M., Rhode K., Ginks M., Delingette H., Rinaldi C.A., Razavi R., and Ayache N. — Coupled Personalization of Cardiac Electrophysiology

Models for Prediction of Ischaemic Ventricular Tachycardia.

Journal of the Royal Society Interface Focus , 2011, 1(3) , 396-407.

[23] Relan J., Pop M., Delingette H., Wright G., Ayache N., and Sermesant M. — Personalisation of a Cardiac Electrophysiology Model using Optical Mapping and MRI for Prediction of Changes with Pacing. IEEE Transactions on Biomedical Engineering , 2011.

[24] Pernod E., Sermesant M., Konukoglu E., Relan J., Delingette H., and Ayache N. — A Multi-Front Eikonal Model of Cardiac Electrophysiology for Interactive Simulation of RadioFrequency Ablation. Computers and Graphics , 2011, 35 , 431-440.

[25] Bestel J., Clément F. and Sorine M. — A Biomechanical Model of Muscle Contraction.

MICCAI. Lecture Notes in Computer Science , 2001, Vol. 2208/2001 , 1159-1161.

[26] Sainte-Marie J., Chapelle D., Cimrman R., and Sorine M. — Modeling and estimation of the cardiac electromechanical activity. Computers & Structures , 2006, vol. 84 , 1743-1759 pp.

[27] Chapelle D., Tallec P. Le, Moireau P., Sorine M. — An energy-preserving muscle tissue model : formulation and compatible discretizations. International Journal of Multiscale Computational Engineering , 2010.

[28] Sermesant M., Delingette H., and Ayache N. — An Electromechanical Model of the Heart for Image Analysis and Simulation. IEEE Transactions in Medical Imaging , 2006, 25(5) , 612-625.

[29] Delingette H., Billet F., Wong K.C.L., Sermesant M., Rhode K., Ginks M., Rinaldi C.A., Razavi R., and Ayache N. — Personalization of Cardiac Motion and Contractility from Images using Variational Data Assimilation. IEEE Trans. in Biomedical Engineering Letters , 2011.

[30] Chabiniok R., Moireau P., Lesault P.F., Rahmouni A., Deux J.-F. and Chapelle D. — Estimation of tissue contractility from cardiac cine-MRI using a biomechanical heart model.

Biomechanics and Modeling in Mechanobiology , 2011.

[31] Sermesant M., Peyrat J.M., Chinchapatnam P., Billet F., Mansi T., Rhode K., Delingette H., Razavi R., and Ayache N. — Toward patient-specific myocardial models of the heart. Heart Failure Clinics , July 2008, 4(3) , 289-301.

[32] Sermesant, Chabiniok R., Chinchapatnam P., Mansi T., Billet F., Moireau P., Peyrat J.M., Wong K., Relan J., Rhode K., Ginks M., Lambiase P., Delingette H., Sorine M., Rinaldi C.A., Chapelle D., Razavi R., and Ayache N. — Patient-Specific Electromechanical Models of the Heart for Prediction of the Acute Effects of Pacing in CRT : a First Validation.

Medical Image Analysis , 2011.

[33] Boulakia M., Gerbeau J.F. — Parameter Identification in Cardiac Electrophysiology Using Proper Orthogonal Decomposition Method. FIMH, LNCS, Springer, 2011.

[34] Ferna´ndez M.A., Formaggia L., Gerbeau J.-F., Quarteroni A. — The derivation of the equations for fluids and structures, In Cardiovascular mathematics , 2009, Vol. 1 of MS&A.

Model. Simul. Appl., Springer Verlag, 77-121 pp.

[35] Mansi T., André B., Lynch M., Sermesant M., Delingette H., Boudjemline Y., and Ayache N. — Virtual pulmonary valve replacement interventions with a personalised cardiac electromechanical model. Recent Advances in the 3D Physiological Human, Proceedings of Functional Imaging and Modeling of the Heart 2009 (FIMH’09), LNCS, 5528, 201-210.

[36] Mansi T., Voigt I., Leonardi B., Pennec X., Durrleman S., Sermesant M., Delingete H., Taylor A.M., Boudjemline Y., Pongiglione G., and Ayache N. — A Statistical Model for Quantification and Prediction of Cardiac Remodelling : Application to Tetralogy of Fallot.

IEEE Transactions on Medical Images , September 2011, 9(30) , 1605-1616.

[37] Konukoglu E., Relan J., Cilingir U., Menze B., Chinchapatnam P., Jadidi A., Cochet H., Hocini M., Delingette H., Jaïs P., Haïssaguerre M., Ayache N., and Sermesant M. —

Efficient Probabilistic Model Personalization Integrating Uncertainty on Data and Parameters : Application to Eikonal — Diffusion Models in Cardiac Electrophysiology. Progress in Biophysics and Molecular Biology , 2011.

[38] McNary T.G., Bridge J.H., and Sachse F.B. — Strain transfer in ventricular cardiomyocytes to their transverse tubular system revealed by scanning confocal microscopy. Biophys J. , 2011, 100(10) , L53-55.

[39] Young A.A. and Frangi A.F. — Computational cardiac atlases : from patient to population and back. Experimental Physiology , 2009, 94 , 578-596.

[40] Ayache N., Clatz O., Delingette H., Malandain G., Pennec X., and Sermesant M. — Vers un patient numérique personnalisé pour le diagnostic et la thérapie guidés par l’image. Médecin / Sciences , Mars 2011, 27 , 208-213.

DISCUSSION

M. Pierre CORVOL

Travaillez-vous sur des modèles animaux (petits rongeurs, porcs) qui permettraient d’affiner ou de valider les modèles que vous proposez ?

En collaboration avec Mihaela Pop du laboratoire du Pr. Graham Wright à Toronto, nous avons procédé à des expériences d’électrophysiologie ex vivo sur des cœurs excisés de lapins et de porcs. L’activité électrique était révélée par des marqueurs fluorescents en imagerie optique. Ces expériences ont permis de valider plusieurs modèles électriques ainsi que des méthodes de personnalisation.

M. André VACHERON

Les perspectives de la modélisation cardiaque sont passionnantes. Michel Haïssaguerre et Pierre Jaïs ont-ils commencé à utiliser ces résultats dans la localisation des foyers arythmogènes des orifices des veines pulmonaires pour le traitement par radiofréquence de la fibrillation auriculaire ?

Nos travaux sur la modélisation en électrophysiologie se concentrent sur la modélisation des ventricules cardiaques. Ils visent la détection et la prédiction des courants de réentrée, et à terme la prédiction du risque de tachycardie/fibrillation ventriculaire. Les premières applications cliniques seraient l’aide à la planification des cibles pour la thermoablation de tissus ventriculaires, ainsi que l’aide à la décision pour la pose de défibrillateurs implantés.

M. Christian CABROL

Va-t-on publier des documents de ce type pour l’instruction des étudiants et des médecins sur la disposition géométrique des fibres myocardiques, bien qu’elle soit bien décrite dans le manuel d’anatomie de Rouvière ? Va-t-on pouvoir utiliser en clinique, les courbes de propagation de l’influx électrique au lieu des cartographies si longues à établir autrefois, comme le faisait mon assistant Gérard Guiraudon le pionnier de la chirurgie des troubles du rythme en Europe ? Quand va-t-on pouvoir utiliser en chirurgie, ces données, pour la correction des anomalies ou des lésions des cavités cardiaques ?

Nous avons rendu accessible sur notre site internet l’atlas numérique 3D des fibres cardiaques construit à partir d’une première base de données d’IRM de diffusion de cœurs canins, (http://www-sop.inria.fr/asclepios/data/heart/) et nous comptons faire de même prochainement pour l’atlas numérique 3D des fibres cardiaques de cœurs humains.

M. Yves LOGEAIS

Vos images sont passionnantes. La simulation sur l’excitation cardiaque et sa propagation a une valeur pédagogique particulière. Je retiens aussi l’image du ventricule droit anormalement grande qui évoque la maladie d’Elestein et les ectasies du ventricule gauche, accessibles à la chirurgie de réduction. De même, l’imagerie du bloc de branche gauche qui pose aussi la question de la quantité myocardique.

Dans le cadre du projet Européen Health-e-Child, nous avons analysé les images de jeunes patients souffrant d’une Tétralogie de Fallot opérée, conduisant à des régurgitations au niveau des valves pulmonaires et à une hypertrophie du ventricule droit. Nous avons utilisé nos modèles biophysiques du cœur pour décrire le bénéfice potentiel d’une intervention chirurgicale.

Bull. Acad. Natle Méd., 2011, 195, no 8, 1855-1868, séance du 22 novembre 2011